éléments de base

Le calcul quantique manipule des vecteurs dans un espace de Hilbert.
Un qubit correspond à un espace de Hilbert de dimension 2
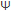|> = a |0>+ ß |1> avec |a|² + |ß|² = 1

L’espace des états d’un système composite est le produit tensoriel des espaces individuels.
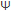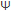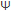|12> = |1>|2>

L’évolution d’un système isolé est représentée par une matrice de transformation unitaire.
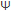|(0)> -> |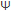(t)> = U(t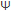,0) |(0)>

Une grandeur physique peut être mesurée grâce à un opérateur hermitien de l'espace de Hilbert. Cette mesure projette le vecteur d'état sur une des valeurs propres avec une probabilité égale à la norme au carré de l'amplitude correspondante.
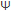|> = a |0>+ ß |1> : la probabilité de mesurer |0> est |a|²